“A teacher is more like a gardener who tends each plant, examines, waters, and sees that the plant may take its own nourishment. The teacher should be a guide, a helper, and a friend. He/she must study the child, must know the effect of the environment on the child, and should know the laws of learning for which a study of psychology is necessary.”

Key requirements in the teaching and learning process
The learner must be active in some way with respect to what is to be learnt, whether it is some kind of information, a skill, an understanding, an attitude etc. Learners are more able to analyse, evaluate and synthesise ideas and thus scale the higher order skills of Bloom’s Taxonomy. Skilled and innovative math teachers make this possible by providing conducive environments, opportunities, interactions, activity based learning which foster deep learning.
Sample 1:
- To understand variables and constants in Algebra
- Technique used: TPS[Think, Pair, and Share]
- Activity sheet: A picture of a city bus ride
- Number of tasks: 3
- Groups: 3

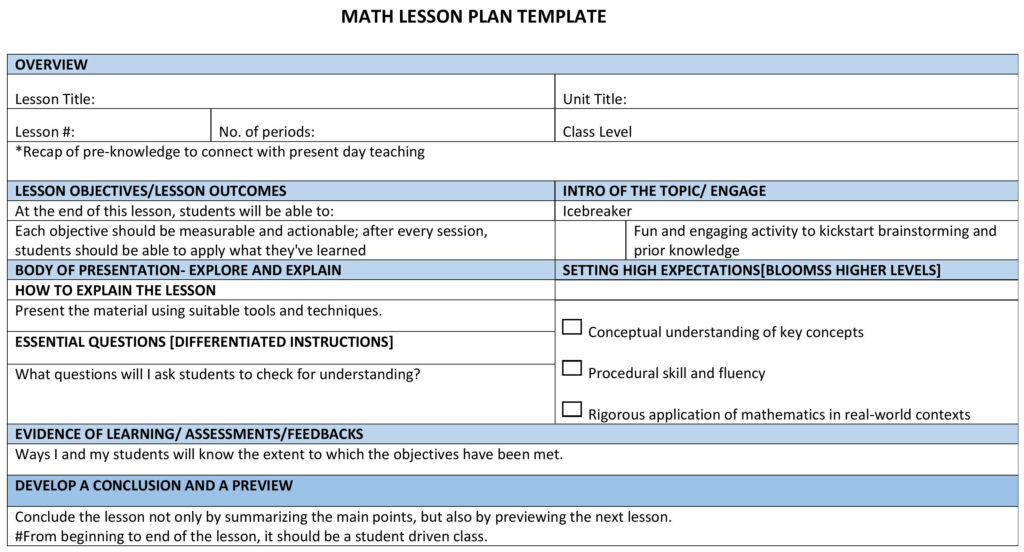
First Task: Think of as many (measurable) quantities that are associated with a city bus ride on a particular route. The group that writes the greatest number of such quantities in two minutes will be the winner.
List of estimated quantities
- Number of passengers in bus
- Driver in bus
- Total fare for a journey to various destinations
- Time taken for a specific journey
- Number of red lights at traffic signals during the journey
- Distance of a journey
- Number of wheels on the bus
- Number of bolts on each wheel of the bus
- Plate number of the bus
- Speed of the bus
- Cost of the bus
- Odometer reading of the bus
- Mileage of the bus
Second task: Find out the quantities in this journey which can change and the quantities that do not change. Allotted time again is two minutes and the winner is decided after the task.
Third task: To introduce x,y,z as variables and numerals as constant in the given example
The bus driver charges $15 for first kilometre and $8 each for every subsequent kilometre. For a total distance of x km an amount of $y is paid. Write the linear equation representing this information.

Explanation:
Now, out of ‘x’ km already 1km is traveled and we know the amount as $15, thus the rest of the travel will be (x – 1) km.
It is said that the total amount is ‘y’ dollars, thus the total will be $15 for the first km and $8 for (x – 1) km. Thus the total amount paid is y and the equation will be,
y = 15 + 8 (x-1)
Now, let us simplify the given expression,
y = 15 + 8x – 8
y = 8x + 7
Thus we got the linear equation representing the equation as,
y = 8x + 7
Follow-up exercise by students:
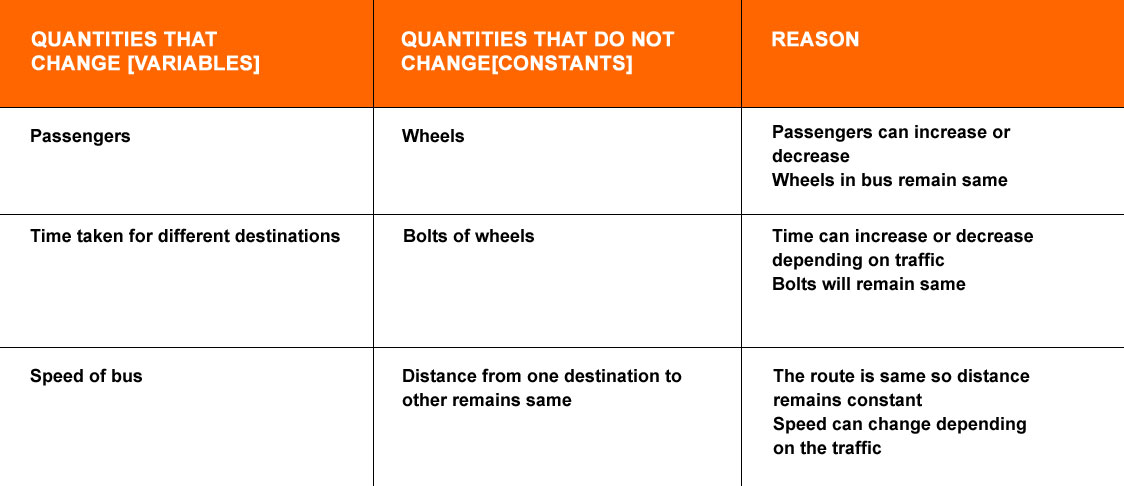
If you assume values for (x, y) in equation y = 8x + 7, can you find the cost and distance traveled by bus in 1km, 2km, 3km, and 4.5km respectively?
| X [distance] | 1 | 2 | 3 | 4.5 |
| Y [$] | 15 | 23 | 31 | 43 |
Principle of repetition:
Repetition under conducive environment in the class results in more permanent learning. Research has shown that “repeating something twenty times over the course of one day is less effective than repeating something ten times over the course of a week.“ A follow-up and practice session is a must in making children learn as well as enjoy math. It can be also re-teaching a topic or sub-topic.
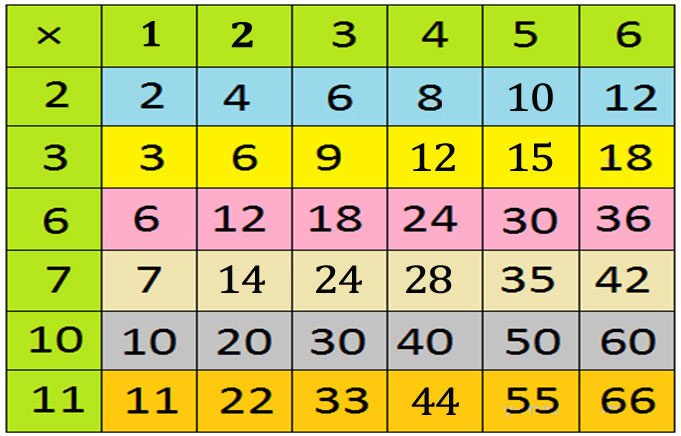
Sample 2: Learning Tables in a simple yet innovative way for beginners.
Follow-up exercise by students:
Max forgot how to fill in the numbers in the grid. Can you help him by filling in the missing numbers?
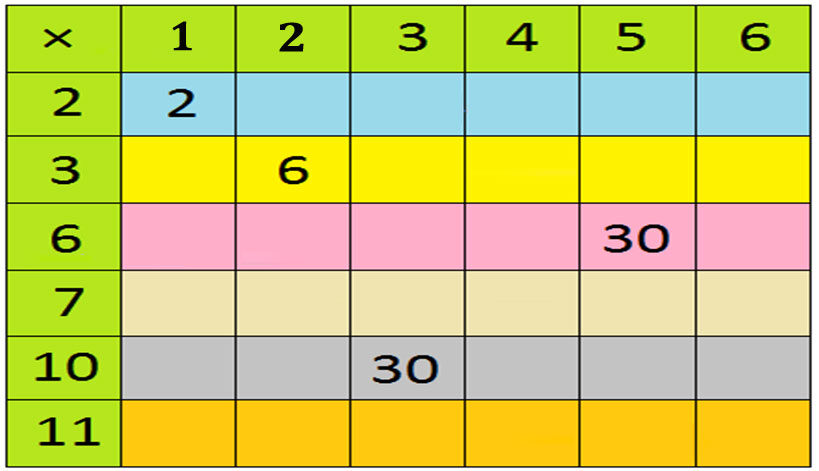
Solution:
Principle of effect, satisfaction or annoyance:
A child learns or remembers best those experiences which are either painful or enjoyable. ”The burnt child dreads the fire.” The immediate effect of learning activity fits in with one of those class activities the learner is engaged. The output of learning becomes more favorable.
Sample 3: A visit to a grocery store to buy a list of things to try out hand in baking a cake or cookies.
- Maximum math can be learnt and experienced in the kitchen. Students can be encouraged and motivated to play math challenges at the grocery store.
- Estimation of total cost of the products prior to final payment to check whether it is within the money limit given by parents.
- Incorporating coupons, sales and discount offers and adjusted pricing for bulk items.
- Settling the final amount in cash and counting back the due amount returned
- Recipe of baking cookies/ cake in terms of measurement of ingredients
- Understanding of ratio and proportion for baking
- Estimation of temperature of oven and even at times conversion from Fahrenheit to Celsius or vice versa as required by the appliance
- Metric conversions to measure a tablespoon, teaspoon or ounce
- The end product will be a beautifully baked cake or cookies by children created out of the messy kitchen. This joy in learning math in a playful way will never be forgotten by children.

Learning and its connection with intelligence:
A teacher should learn the limits of each individual in the class(I.Q) and the mental ability stage and adopt techniques of teaching accordingly. For eg. teaching a slow or non-enthusiastic learner needs concrete sensory aids and lot of activities; for bright students there must be challenges in the form of puzzles, abstract materials and methods calling for creativeness. This is called differential instruction.It is the most essential and basic responsibility of the teacher to engage their pupils in the appropriate kind of learning activities with sufficient ardour and attention to assure substantial learning.
-
Give a start to the class by knocking on students’ prior knowledge
It is always suggested to proceed with known to unknown -
Gain an understanding of students’ interest
A teacher should know the learning strengths of every child like practical, creative and analytical intelligence so that the fear of math in the child can be easily eliminated by engaging him in the activities of his strength. -
Organize collaborative group discussions
Group activities make the non enthusiastic children feel secured
-
Design relevant differential instructions
Differentiated worksheets and activities to boost up the confidence of the ones who fear math. Each group of students get different levels of problem sums to solve based on their learning styles -
Integrate modern technology
Multimedia like videos, animations, films ,you tube and digital technology like simulations, different apps can bring revolution in learning math -
Provide timely and regular feedback in terms of progress
An encouraging feedback can motivate the child to enhance his performance.
Sample 4:
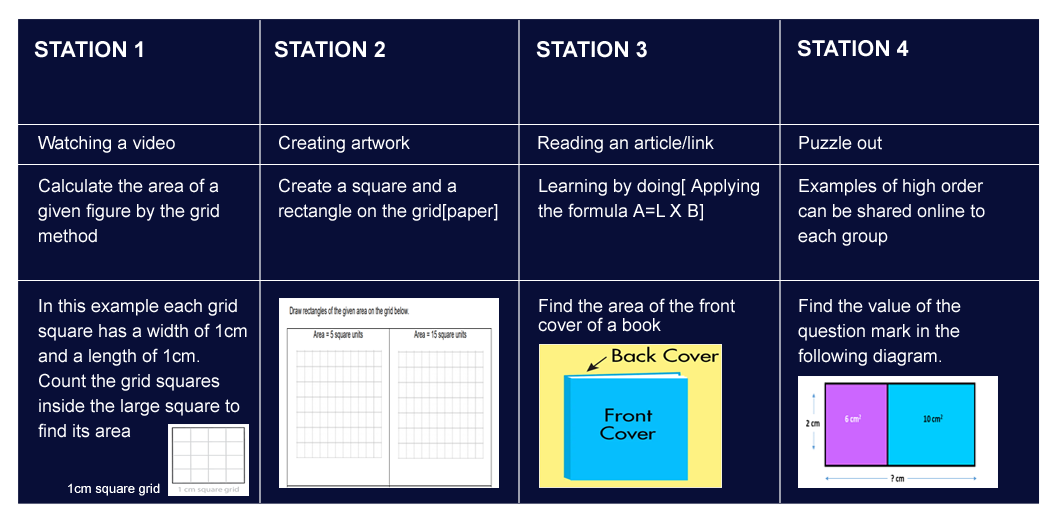
The topic area of squares and a rectangle is introduced in a class by differential methods of instruction, based on students 'learning styles. Four learning stations are created and students are divided into 4 groups depending on the strength of the class through which the teams rotate.
- Google forms: This allow students to see which questions they got correct/incorrect. They can revise their answers after submitting, which is a great option if another similar quiz is given to them
- Peer feedback: Exchange of work between peers gives an immediate insight into the understanding of concepts taught in class.
- Exit slips: Student responses to questions posed at the end of a class or lesson. These quick, informal assessments enable teachers to quickly assess students' understanding of the material.
- Self-Assessment rubrics: A scoring tool that identifies the various criteria relevant to a learning outcome and action taken accordingly to make a student master the concept which needs attention
- Personal feedback[verbal, audio, written]: Actionable or descriptive feedback in math supports student learning
Proper lesson plan:
A rough drafting of the maths topics to be taught should be planned beforehand. It creates self-confidence in the topic and the students to be taught. The various steps include:
- Specific aims-objectives of the topics to be taught
- Learning outcome/success criteria after each topic taught
- Recapitulation-connecting to previous knowledge
- Introduction of the topic/ icebreaker/Engage
- Body of presentation- Explore and Explain
- Instruction-guided, independent
- Generalization-summary/oral recapitulation
- Continuous feedback-Evaluate/assess
- Home assignment-extension of CW/ Research activity